探索数学的奥秘——函数定义的奇幻之旅
亲爱的数学爱好者们,你是否曾在深夜里仰望星空,想象着那些抽象的数学符号背后隐藏的神奇世界?今天,就让我们一起踏上这场探索函数定义的奇幻之旅吧!
一、函数的诞生
在遥远的古代,数学家们对世界充满了好奇。他们发现,在自然界中,许多现象都可以用数量关系来描述。比如,月亮的圆缺、太阳的升起落下,甚至我们的心跳、呼吸,都遵循着一定的规律。于是,函数这个概念应运而生。

二、函数的定义
那么,什么是函数呢?简单来说,函数就是两个变量之间的关系。在这个关系中,一个变量(我们称之为自变量)的每一个值,都对应着另一个变量(我们称之为因变量)的唯一值。
在数学上,我们可以用以下方式来定义函数:
设A和B是两个非空集合,如果按照某种对应关系,对A中的每一个元素,在B中都有唯一确定的元素与之对应,那么我们就称这种对应关系为函数,记作f: A → B。
这里的f表示函数,A表示定义域,B表示值域。也就是说,函数f将集合A中的每一个元素映射到集合B中的唯一元素。
三、函数的类型
函数有很多种类型,其中最常见的一次函数、二次函数、指数函数、对数函数等。下面,我们就来简单介绍一下这些函数的特点。
1. 一次函数:形如y = ax b的函数,其中a和b是常数,且a ≠ 0。一次函数的图像是一条直线,斜率a表示直线的倾斜程度,截距b表示直线与y轴的交点。
2. 二次函数:形如y = ax^2 bx c的函数,其中a、b、c是常数,且a ≠ 0。二次函数的图像是一个抛物线,开口方向由a的符号决定,顶点坐标为(-b/2a, c - b^2/4a)。
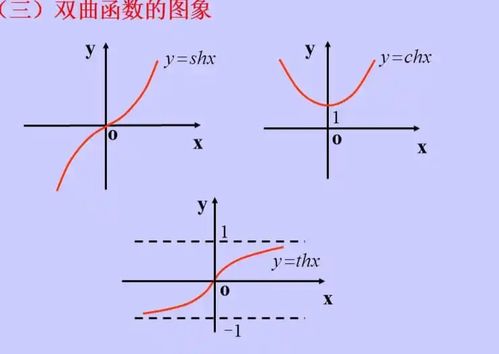
3. 指数函数:形如y = a^x的函数,其中a是常数,且a > 0,a ≠ 1。指数函数的图像是一个不断上升或下降的曲线,斜率随着x的增加而增大或减小。
4. 对数函数:形如y = log_a(x)的函数,其中a是常数,且a > 0,a ≠ 1。对数函数的图像是一个不断上升的曲线,斜率随着x的增加而增大。
四、函数的应用
函数在现实生活中有着广泛的应用。比如,我们可以用函数来描述物体的运动轨迹、物体的生长规律、经济变化等。以下是一些常见的应用场景:
1. 物理学:描述物体的运动轨迹、速度、加速度等。
2. 生物学:描述生物的生长、繁殖、死亡等规律。
3. 经济学:描述商品的价格、供需关系、经济增长等。
4. 工程学:描述电路、建筑、机械等的设计和运行。
五、函数的拓展
随着数学的发展,函数的概念也在不断拓展。比如,我们可以将函数推广到复数域、向量空间等更广泛的领域。此外,还有一些特殊的函数,如概率分布函数、随机变量函数等,它们在统计学、概率论等领域有着重要的应用。
在这个奇幻的数学世界里,函数就像一位神奇的魔法师,将抽象的数学符号变成了丰富多彩的现实世界。让我们一起继续探索,揭开更多数学奥秘的面纱吧!
亲爱的读者们,你是否对函数的定义有了更深入的了解呢?希望这篇文章能为你带来启发,让你在数学的海洋中畅游无阻!
